|
Uma visão geral sobre sequências
Uma sequência real é uma função f definida sobre o conjunto N={1,2,3,4,...} dos números naturais.
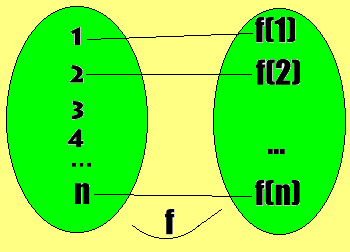
Uma sequência é uma função cujo domínio é o conjunto N e cuja imagem está contida em R (conjunto dos números reais).
Muitas vezes, a sequência (função) é confundida com a Imagem da função (conjunto de números), no entanto, esta confusão até mesmo colabora para o entendimento do significado de uma sequência no âmbito do Ensino Médio.
Um fato importante é que a função determina a regra que os elementos do conjunto imagem devem seguir.
Na sequência, apresentaremos exemplos de sequências reais e os seus respectivos conjuntos imagens.
- Sequência natural
A imagem é representada pelo conjunto dos números naturais.
f : N  R definida por f(n) = n R definida por f(n) = n
Im(f) = { 1, 2, 3, 4, 5, ... }
- Sequência dos inversos
A imagem é representada pelo conjunto dos inversos dos números naturais.
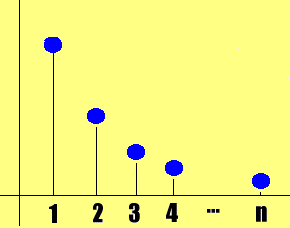
f : N  R definida por f(n) = 1/n R definida por f(n) = 1/n
Im(f) = { 1, 1/2, 1/3, 1/4, 1/5, ... }
- Sequência constante
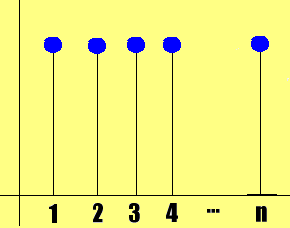
A imagem é representada por um conjunto unitário.
f : N  R definida por f(n) = 2 R definida por f(n) = 2
Im(f) = { 2, 2, 2, 2, ... } = { 2 }
- Sequência alternada
A imagem é representada por um conjunto de números que fica alternando o sinal, sendo que um é negativo e o subsequente positivo, e assim por diante.
f : N  R definida por f(n) = (-1)n n R definida por f(n) = (-1)n n
Im(f) = { -1, +2, -3, +4, -5, +6, ... }
- Sequência aritmética
Cada termo do conjunto imagem é a soma do anterior com um número fixo denominado razão.
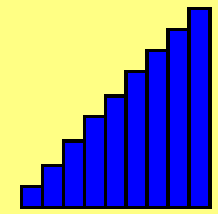
f : N  R definida por f(n) = a1 + (n-1).r R definida por f(n) = a1 + (n-1).r
Im(f) = { a1, a1+r, a1+2r, a1+3r, ..., a1+(n-1)r, ...}
- Sequência geométrica
Cada termo do conjunto imagem é o produto do anterior por um número fixo denominado razão.
f : N  R definida por f(n) = a1.qn-1 R definida por f(n) = a1.qn-1
Im(f) = { a1, a1q,
a1q2, a1q3, ..., a1qn-1, ...}
- Sequência de Fibonacci
A imagem é representada por um conjunto de tal forma que cada elemento a partir do terceiro é a soma dos dois anteriores.
f : N  R definida por f(n+2) = f(n+1) + f(n), f(1)=f(2)=1 R definida por f(n+2) = f(n+1) + f(n), f(1)=f(2)=1
Im(f) = { 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... }
A sequência de Fibonacci é um exemplo de uma sequência recursiva, isto é, uma sequência que é definida em função de seus termos anteriores.
Média aritmética
Dados n números reais x1, x2, x3, ..., xn, definimos a média aritmética entre estes números, denotada pela letra x com um traço sobre a mesma, como a divisão entre a soma desses números e o número de elementos, isto é:
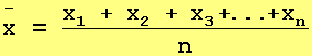
Média geométrica
Dados n números reais positivos x1, x2, x3, ..., xn, definimos a média geométrica entre estes números, denotada pela letra g, como a raiz n-ésima do produto entre estes números, isto é:
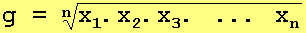
Antecedente é o termo que está imediatamente antes do termo sob análise e consequente é o termo que fica imediatamente após o elemento sob análise.
Na sequência aritmética, cada termo é a média aritmética entre o antecedente e o consequente do termo tomado, enquanto na sequência geométrica, cada termo é a média geométrica entre o antecedente e o consequente do termo tomado, daí a razão de tais denominações para estas sequências.
As sequências aritméticas e geométricas são muito estudadas no âmbito do Ensino Médio sob o nome de "Progressões aritméticas e geométricas".
As sequência geométricas são aplicadas a estudos para a obtenção do montante de um valor capitalizado periodicamente, assim como em estudos de Taxas de juros, Financiamentos e Prestações. Tais sequências também aparecem em estudos de decaimento radioativo (teste do Carbono 14 para a análise da idade de um fóssil ou objeto antigo).
No Ensino Superior tais sequências aparecem em estudos de Sequências e Séries de números e de funções, sendo que a série geométrica (um tipo de sequência obtida pelas somas de termos de uma sequência geométrica) é muito importante para a obtenção de outras séries.
As sequências de Fibonacci aparecem de uma forma natural em estudos de Biologia, Arquitetura, Artes e Padrões de beleza. O livro "A divina proporção", Huntley, Editora Universidade de Brasília, trata do assunto.
Sequências aritméticas
Uma sequência aritmética já foi definida antes e é normalmente escrita na forma:

O primeiro termo de uma sequência é indicado por a1 e o n-ésimo termo por an e como a diferença entre dois termos consecutivos é a razão r, temos que:
| a2 - a1 |
= |
r |
| a3 - a2 |
= |
r |
| a4 - a3 |
= |
r |
| ... |
= |
... |
| an-1 - an-2 |
= | r |
| an - an-1 |
= |
r |
Como temos n-1 linhas então, somando membro a membro os elementos da primeira coluna e da terceira coluna e realizando os cancelamentos possíveis, obteremos:
an - a1 = (n-1).r
e temos a fórmula do termo geral de uma sequência aritmética:
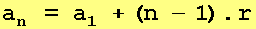
Observemos a sequência aritmética tomada como exemplo:
: 1 . 3 . 5 . 7 . 9 . 11 . 13 . ... 101.
Neste caso:
Pode-se perguntar:
- Qual é o número de termos desta "PA" ?
- Qual é o trigésimo termo desta "PA" ?
Para resolver este problema, basta utilizar a fórmula do termo geral, para obter
n = 51
e
a30 = 59
Observemos que no caso da sequência apresentada, a soma dos extremos é igual a 102, a soma do segundo termo com o penúltimo termo é também 102, a soma do terceiro termo com o ante-penúltimo termo é 102, e em geral, a soma de termos equidistantes dos extremos é sempre igual a
a1 + an.
Em geral, em uma PA, temos:
a1+an = a2+an-1 = a3+an-2 = ... = an-2+a3 = an-1+a2 = an+a1
Obteremos agora a fórmula para a soma dos n termos de uma sequência aritmética.
Se
S = a1 + a2 + a3 + ... + an-2 + an-1 + an
então
S = an + an-1 + an-2 + ... + a3 + a2 + a1
logo
2S = (a1 + an) + (a2+an-1) + ... + (an + a1)
assim
2S = n.(a1+ an)
Temos então a fórmula da soma dos termos de uma PA:
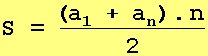
Sequências geométricas
Uma sequência geométrica já definida antes e é normalmente escrita na forma:
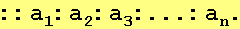
Como a divisão (quociente) entre dois termos consecutivos é a razão q, temos que:
| a2 / a1 |
= |
q |
| a3 / a2 |
= |
q |
| a4 / a3 |
= |
q |
| ... |
= |
... |
| an-1 / an-2 |
= | q |
| an / an-1 |
= | q |
Como temos n-1 linhas então, multiplicando membro a membro os elementos da primeira coluna e da terceira coluna e realizando os cancelamentos possíveis, obteremos:
an / a1 = qn-1
e temos a fórmula do termo geral de uma sequência geométrica:
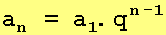
Observemos como exemplo a sequência aritmética:
: 2 . 4 . 8 . 16 . 32 . ... 1024.
Neste caso:
Pode-se perguntar:
- Qual é o número de termos desta "PG" ?
- Qual é o oitavo termo desta "PG" ?
Para resolver este problema, basta utilizar a fórmula do termo geral, para obter
n = 10
e
a8 = 256
De forma similar ao que ocorre com as sequências aritméticas, observemos que no caso da sequência apresentada, o produto dos extremos é igual a 2048, o produto do segundo termo com o penúltimo termo é também 2048, o produto do terceiro termo com o ante-penúltimo termo é 2048, e em geral, o produto de termos equidistantes dos extremos é sempre igual a
a1 . an.
Obteremos agora a fórmula para a soma dos n termos de uma sequência geométrica.
Se
S = a1 + a2 + a3 + ... + an-2 + an-1 + an
então, multiplicando todos os termos da igualdade acima pela razão q, teremos:
q.S = q.a1 + q.a2 + q.a3 + ... + q.an-2 + q.an-1 + q.an
e esta última expressão pode ser escrita como:
q.S = a2 + a3 + ... + an-1 + an + q.an
assim
q.S = S - a1 + q.an
ou seja
q.S - S = q.an - a1
Obtendo o valor de S na expressão acima, obtemos:
S = (q.an - a1) / (q-1)
que pode ser reescrita como:
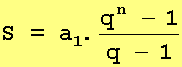
Exercício
Você conhece alguma sequência que cada termo é a média harmônica dos termos antecedente e consequente?
Projeto MatWeb: Matemática pela Internet
Página construída por Ulysses Sodré
Atualizada em: October 05, 2000.
|