Elementos básicos para a construção de matrizes
Aqui tomaremos o conjunto N dos números naturais, como:
N = { 1, 2, 3, 4, 5, 6, 7, ...}
O produto cartesiano N×N indicará o conjunto de todos os pares ordenados da forma (a,b), onde a e b são números naturais, isto é:
N×N = {(a,b) : a e b são números naturais}
Uma relação importante em N×N é:
Smn = {(i,j): 1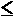 i i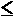 m, 1 m, 1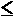 j j 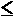 n} n}
Definição de matriz
Uma matriz real (complexa) é uma função que a cada par ordenado (i,j) no conjunto Smn associa um número real (complexo).
Uma forma muito comum e prática para representar uma matriz
definida na forma acima é através de uma tabela contendo m x n números reais (ou complexos). Identificaremos a matriz abaixo com a letra A.
| a(1,1) | a(1,2) | ... | a(1,n) |
|---|
| a(2,1) | a(2,2) | ... | a(2,n) |
|---|
| ... | ... | ... | ... |
|---|
| a(m,1) | a(m,2) | ... | a(m,n) |
|---|
Observações sobre matrizes
- Se a matriz A tem m linhas e n colunas, dizemos que a ordem da matriz é mxn.
- Na tabela acima a posição de cada elemento aij = a(i,j) é indicada pelo par ordenado (i,j).
- Indicamos uma matriz A pelos seus elementos como: A=[a(i,j)].
- A diagonal principal da matriz é indicada pelos elementos da forma a(i,j) onde i=j.
- Matriz quadrada é a que tem o número de linhas igual ao número de colunas, i.e., m=n.
- A diagonal secundária de uma matriz quadrada de ordem n é indicada pelos n elementos:
a(1,n), a(2,n-1), a(3,n-2), a(4,n-3), a(5,n-4), ..., a(n-1,2), a(n,1)
- Matriz diagonal é a que tem elementos nulos fora da diagonal principal.
- Matriz real é aquela que tem números reais como elementos.
- Matriz complexa é aquela que tem números complexos como elementos.
- Matriz nula é aquela que possui todos os elementos iguais a zero.
- Matriz identidade , denotada por Id, tem os elementos da diagonal principal iguais a 1 e zero fora da diagonal principal.
- Matriz diagonal é aquela que tem todos os elementos nulos fora da diagonal principal. Alguns elementos da diagonal principal podem ser nulos.
Exemplos interessantes de matrizes:
Matriz 4x4 de números reais:
| 12 |
-6 |
7 |
18 |
| -23 |
-24 |
0 |
0 |
| 0 |
0 |
5 |
0 |
| 0 |
0 |
0 |
9 |
Matriz 4x4 de números complexos:
| 12 |
-6+i |
7 |
i |
| -i |
-24 |
0 |
0 |
| 0 |
0 |
5+i |
5-i |
| 0 |
0 |
0 |
9 |
Matriz nula com duas linhas e duas colunas:
Matriz nula com três linhas e duas colunas:
Matriz identidade com três linhas e três colunas:
Matriz diagonal com quatro linhas e quatro colunas:
Matrizes iguais
Duas matrizes A=[a(i,j)] e B=[b(i,j)], de mesma ordem mxn, são iguais se todos os seus correspondentes elementos são iguais, isto é:
a(i,j) = b(i,j)
para todo par ordenado (i,j) em Smn.
Exercício: Determinar os valores de x e y para que sejam iguais as matrizes abaixo, isto é:
Soma de matrizes
A soma (adição) de duas matrizes A=[a(i,j)] e B=[b(i,j)] de mesma ordem mxn, é uma outra matriz C=[c(i,j)], definida por:
c(i,j) = a(i,j) + b(i,j)
para todo par ordenado (i,j) em Smn.
Exemplo: A soma das matrizes A e B é a terceira matriz indicada abaixo.
Propriedades da soma de matrizes
A1: Associativa
Para quaisquer matrizes A, B e C, de mesma ordem mxn, vale a igualdade:
(A + B) + C = A + (B + C)
A2: Comutativa
Para quaisquer matrizes A e B, de mesma ordem mxn, vale a igualdade:
A + B = B + A
A3: Elemento neutro
Existe uma matriz nula 0 que somada com qualquer outra matriz A de mesma ordem, fornecerá a própria matriz A, isto é:
0 + A = A
A4: Elemento oposto
Para cada matriz A, existe uma matriz -A, denominada a oposta de A, cuja soma entre ambas fornecerá a matriz nula de mesma ordem, isto é:
A + (-A) = 0
Multiplicação de escalar por matriz
Seja k um escalar e A=[a(i,j)] uma matriz. Definimos a multiplicação do escalar k pela matriz A, como uma outra matriz C=k.A, definida por:
c(i,j) = k. a(i,j)
para todo par ordenado (i,j) em Smn.
Exemplo: A multiplicação do escalar -4 pela matriz A, definida por:
Propriedades da multiplicação de escalar por matriz
E1: Multiplicação pelo escalar 1
A multiplicação do escalar 1 por qualquer matriz A, fornecerá a própria matriz A, isto é:
1.A = A
E2: Multiplicação pelo escalar zero
A multiplicação do escalar 0 por qualquer matriz A, fornecerá a matriz nula, isto é:
0.A = 0
E3: Distributividade das matrizes
Para quaisquer matrizes A e B de mesma ordem e para qualquer
escalar k, tem-se:
k.(A+B) = k.A + k.B
E4: Distributividade dos escalares
Para qualquer matriz A e para quaisquer escalares p e q, tem-se:
(p+q).A = p.A + q.A
Multiplicação de matrizes
Seja a matriz A=[a(i,j)] de ordem mxn e a matriz B=(b(k,l)) de ordem nxr. Definimos o produto das matrizes A e B como uma outra matriz C=A.B, definida por:
c(u,v) = a(u,1).b(1,v) + a(u,2).b(2,v) + ... + a(u,m).b(m,v)
para todo par (u,v) em Smr.
Para obter o elemento da 2a. linha e 3a. coluna da matriz produto C=A.B, isto é, o elemento c(2,3), devemos:
- multiplicar os primeiros elementos da 2a. linha e 3a. coluna;
- multiplicar os segundos elementos da 2a. linha e 3a. coluna;
- multiplicar os terceiros elementos da 2a. linha e 3a. coluna;
- multiplicar os quartos elementos da 2a. linha e 3a. coluna;
- somar os quatro produtos obtidos anteriomente.
Assim:
c23 = a21.b13 + a22.b23 + a23.b33 + a24.b43
Podemos visualizar esta operação através das matrizes seguintes. Basta observar a linha em azul na primeira matriz, a coluna em azul na segunda matriz e o elemento em azul na terceira matriz.
| a11 | a12 | a13
| a14 |
|---|
| a21 |
a22 |
a23 |
a24 |
| a31 | a32 | a33
| a34 |
|---|
| a41 | a42 | a43 | a44 |
|---|
| × |
| b11 | b12 |
b13 | b14 |
|---|
| b21 | b22 |
b23 | b24 |
|---|
| b31 | b32 |
b33 |
b34 |
|---|
| b41 | b42 |
b43 | b44 |
|---|
|
= |
| c11 | c12 | c13
| c14 |
|---|
| c21 | c22 |
c23 | c24 |
|---|
| c31 | c32 | c33
| c34 |
|---|
| c41 | c42 | c43
| c44 |
|---|
|
Observação: Somente podemos multiplicar duas matrizes se o número de
colunas da primeira for igual ao número de linhas da segunda.
Propriedades da multiplicação de matrizes
Para todas as matrizes A, B e C que podem ser multiplicadas, temos algumas propriedades:
M1: Nem sempre vale a comutatividade
Em geral, A×B é diferente de B×A, como é o caso do produto que segue, onde A está cor vermelha e B em cor preta:
M2: Distributividade da soma à direita
A.(B+C) = A.B + A.C
M3: Distributividade da soma à esquerda
(A+B).C = A.C + B.C
M4: Associatividade
A.(B.C) = (A.B).C
M5: Nulidade do produto
Pode acontecer que o produto de duas matrizes seja a matriz nula, isto é: A.B = 0, embora nem A nem B sejam matrizes nulas, como é o caso do produto:
M6: Nem sempre vale o cancelamento
Se ocorrer a igualdade A.C = B.C, então nem sempre será verdadeiro que A = B, pois existem exmplos de matrizes como as apresentadas abaixo, tal que:
mas as matrizes A e B são diferentes.
Matrizes com propriedades especiais
- Uma matriz A é nilpotente de índice k natural, se:
Ak = 0
- Uma matriz A é periódica de índice k natural, se:
Ak+1= A
- Uma matriz A é idempotente, se:
A2 = A
- As matrizes A e B são comutativas, se:
A.B = B.A
- As matrizes A e B são anti-comutativas, se:
A.B = - B.A
- A matriz identidade Id multiplicada por toda matriz A, fornecerá a própria matriz A, quando o produto fizer sentido.
Id . A = A
- A matriz A será a inversa da matriz B, se:
A.B =Id
e
B.A = Id
A transposta de uma matriz
Dada uma matriz A=[a(i,j)] de ordem mxn, definimos a transposta da matriz A como a matriz
At = A[(j,i)]
e se observa aqui, que as linhas de A se transformam nas colunas de At.
Propriedades das matrizes transpostas
T1: A transposta da transposta da matriz é a própria matriz.
(At)t = A
T2: A transposta da multiplicação de um escalar por uma matriz é igual ao próprio escalar multiplicado pela transposta da matriz.
(kA)t= k(At)
T3: A transposta da soma de duas matrizes é a soma das transpostas dessas matrizes.
(A+B)t = At + Bt
T4: A transposta do produto de duas matrizes é igual ao produto das transpostas das matrizes na ordem trocada.
(A.B)t = Bt.At
Matrizes simétricas e anti-simétricas
Uma matriz A é simétrica se é uma matriz quadrada tal que:
At = A
Uma matriz A é anti-simétrica se é uma matriz quadrada tal que:
At = -A
Propriedades das matrizes simétricas e anti-simétricas
S1: Se A é uma matriz simétrica de ordem n, então para todo escalar k, a matriz k.A é simétrica.
S2: Se A é uma matriz quadrada de ordem n, então a matriz B = A + At é simétrica.
S3: Se A é uma matriz quadrada de ordem n, então a matriz B = A - At é anti-simétrica.
S4: Se A é uma matriz quadrada de ordem n, então A sempre pode ser decomposta como a soma de uma matriz simétrica S com uma matriz anti-simétrica T, isto é, A = S + T, e neste caso:
S =(1/2)(A + At)
T =(1/2)(A - At)
Projeto MatWeb: Matemática pela Internet
Página construída por Ulysses Sodré
Atualizada em: September 30, 2000 10:50 AM.
|