|
Projeto MatWeb |
Ensino Médio: mod213 | ||
|---|---|---|---|
| Números Complexos | |||
| �ndice Principal - Ensino M�dio |
Na resolução de uma equação algébrica, um fator fundamental é o conjunto universo que representa o contexto onde poderemos encontrar as soluções. Por exemplo, se estivermos trabalhando no conjunto dos números racionais, a equação 2x+7=0, terá uma única solução dada por:
assim, o conjunto solução será:
no entanto, se estivermos procurando por um número inteiro como resposta, o conjunto solução será o conjunto vazio, isto é:
Analogamente, se tentarmos obter o conjunto solução para a equação x2+1=0 sobre o conjunto dos números reais, teremos como resposta o conjunto vazio, isto é:
o que significa que não existe um número real que elevado ao quadrado seja igual a -1, mas se seguirmos o desenvolvimento da equação pelos métodos comuns, obteremos:
onde ![]() é a raiz quadrada do número real -1. Isto parece não ter significado prático e foi por esta razão que este número foi chamado imaginário, mas o simples fato de substituir
é a raiz quadrada do número real -1. Isto parece não ter significado prático e foi por esta razão que este número foi chamado imaginário, mas o simples fato de substituir ![]() pela letra i (unidade imaginária) e realizar operações como se estes números fossem polinômios, faz com que uma série de situações tanto na Matemática como na vida, tenham sentido prático de grande utilidade e isto nos leva à teoria dos números complexos.
pela letra i (unidade imaginária) e realizar operações como se estes números fossem polinômios, faz com que uma série de situações tanto na Matemática como na vida, tenham sentido prático de grande utilidade e isto nos leva à teoria dos números complexos.
Número complexo é todo número que pode ser escrito na forma
onde a e b são números reais e i é a unidade imaginária. O número real a é a parte real do número complexo z e o número real b é a parte imaginária do número complexo z, denotadas por:
Exemplos de tais números são apresentados na tabela.
| Número complexo | Parte real | Parte imaginária |
|---|---|---|
| 2 + 3 i | 2 | 3 |
| 2 - 3 i | 2 | -3 |
| 2 | 2 | 0 |
| 3 i | 0 | 3 |
| -3 i | 0 | -3 |
| 0 | 0 | 0 |
Observação : O conjunto de todos os números complexos é denotado pela letra C e o conjunto dos números reais pela letra R. Como todo número real x pode ser escrito como um número complexo da forma z=x+yi, onde y=0 então assumiremos que o conjunto dos números reais está contido no conjunto dos números complexos.
Para que os números complexos z=2+yi e w=c+3i sejam iguais, deveremos ter que c=2 e y=3.
O oposto de z=-2+3i é o número complexo -z=2-3i.
O conjugado de z = 2-3i é o número complexo z- = 2+3i.
Dados os números complexos z=a+bi e w=c+di, podemos definir duas operações fundamentais, adição e produto, agindo sobre eles da seguinte forma:
Observação : Estas operações nos lembram as operações com expressões polinomiais, pois a adição é realizada de uma forma semelhante, isto é: (a+bx) + (c+dx) = (a+c)+(b+d)x e a multiplicação (a+bx).(c+dx), é realizada através de um algoritmo que aparece na forma:
| a + b x |
| c + d x X |
| ac + bcx |
| adx + bdx2 |
| ac +(bc+ad)x + bdx2 |
de forma que devamos trocar x2 por -1.
Exemplos:
Se z=2+3i e w=4-6i, então
Se z=2+3i e w=4-6i, então
da unidade imaginária
Quando tomamos i =
Pela tabela acima podemos observar que as potência de i cujos expoentes são múltiplos de 4, fornecem o resultado 1, logo toda potência de i pode ter o expoente decomposto em um múltiplo de 4 mais um resto que poderá ser 0, 1, 2 ou 3. Dessa forma podemos calcular rapidamente qualquer potência de i, apenas conhecendo o resto da divisão do expoente por 4.
Exercício: Calcular os valores dos números complexos: i402, i4033 e i1998
Como exemplo:
Ao pensar um número complexo z=a+bi como um vetor z=(a,b) no plano cartesiano, a multiplicação de um número complexo z=a+bi pela unidade imaginária i, resulta em um outro número complexo w=-b+ai, que formi um ângulo reto (90 graus) com o número complexo z=a+bi dado.
Exercício: Tomar um número complexo z, multiplicar por i para obter z1=i.z, depois multiplicar o resultado z1 por i para obter z2=i.z1. Continue multiplicando os resultados obtidos por i até ficar cansado ou então use a inteligência para descobrir algum fato geométrico significativo neste contexto. Após constatar que você é inteligente, faça um desenho no plano cartesiano contendo os resultados das multiplicações.
Dado um número complexo z=a+bi, não nulo (a ou b deve ser diferente de zero) podemos definir o inverso deste número complexo como o número
z-1=u+iv, tal que
O produto de z pelo seu inverso z-1 deve ser igual a 1, isto é:
o que nos leva a um sistema com duas equações e duas incógnitas:
Este sistema pode ser resolvido pela regra de Cramér e possui uma única solução (pois a ou b são
diferentes de zero), fornecendo:
assim, o inverso do número complexo z=a+bi é:
Exemplo: O inverso do número complexo z=5+12i é
Obtenção do inverso de um número complexo: Para obter o inverso de um número complexo, por exemplo, o inverso de z=5+12i, deve-se :
Observação
: Na última igualdade (proporção) o produto dos meios é igual ao produto dos extremos.
A diferença entre os números complexos z=a+bi e z=a+bi é definida como o número complexo obtido pela soma entre z e -w,(isto é:
Exemplo: A diferença entre os complexos z=2+3i e w=5+12i, é:
A divisão entre os números complexos z=a+bi e w=c+di (w não nulo) é definida como o número complexo obtido pelo produto entre z e
w-1, isto é:
Exemplo: Para dividir o número complexo z=2+3i por w=5+12i, basta multiplicar o numerador e também o denominador da fração z/w pelo conjugalo de w:
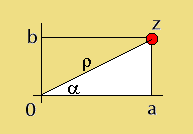
Um número complexo da forma z=a+bi, pode ser
repzesentado geometricamente no plano cartesiano, como sendo um ponto
(par ordenado) tomando-se a abscissa deste ponto como a parte real do
número complexo a no eixo OX e a ordenada como a parte
imaginária do número complexo z no eixo OY, sendo que o
número complexo 0=0+0i é representado pela própria origem (0,0) do sistema.
No gráfico anterior podemos observar que existe um triângulo retângulo cuja hipotenusa correspondente à distância entre a origem 0 e o número complexo z, normalmente denotada pela letra grega ro, o cateto horizontal tem comprimento igual à parte real a do número complexo e o cateto vertical corresponde à parte imaginária b do número complexo z.
Desse modo, se z = a + b i é um número complexo, então:
e a medida da hipotenusa será por definição, o módulo do número complexo z, denotado por |z|, isto é:
O ângulo formado entre o segmento OZ e o eixo OX, aqui representado pela letra grega alfa, é denominado o argumento do número complexo z. Pelas definições da trigonometria circular temos as três relações:
Por experiências com programação na Internet, observei que é melhor usar o cosseno ou o seno do ângulo para definir bem o argumento, uma vez que a tangente apresenta alguns problemas.
Das duas primeiras relações trigonométricas apresentadas anteriormente, podemos escrever:
e assim temos a forma polar do número complexo z:
Consideremos os números complexos
onde, respectivamente, r e s são os módulos e m e n são os argumentos destes números complexos z e w.
Podemos realizar o produto entre estes números
da forma usual e depois reescrever este produto na forma:
Este fato é garantido pelas relações:
Seguindo o produto acima, poderemos obter a potência de ordem k de um número complexo. Como
então
Exemplo: Consideremos o número complexo z=1+i, cujo módulo é igual à raiz quadrada de 2 e o argumento é igual a 1/4 de pi (45 graus). Para elevar este número à potência 16, basta escrever:
Um ponto fundamental que valoriza a existência dos números complexos é a possibilidade de extrair a raiz de ordem 4 de um número complexo, mesmo que ele seja um número real negativo, o que significa, resolver uma
equação algébrica do 4o. grau. Por exemplo, para extrair a raiz quarta do número -16, basta encontrar as quatro raízes da equação algébrica x4+16=0.
Antes de seguir em nosso processo para a obtenção da raiz quarta de um número complexo w, necessitamos antes de tudo, saber o seu módulo r e o seu argumento
t, o que significa poder escrever:
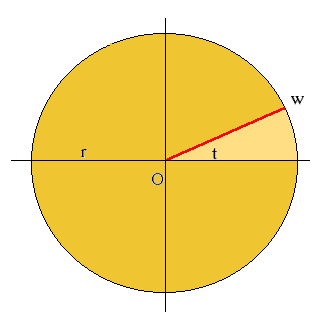
O primeiro passo é realizar um desenho mostrando es|e número complexo w em um círculo de raio r e observar o argumento t, dado pelo angulo entre o eixo OX e o número complexo w.
O passo seguinte é obter um outro número complexo z1 cujo módulo seja a raiz quarta de r e cujo argumento seja t/4.
Este número complexo é a primeira das quatro
raizes complexas procuradas.
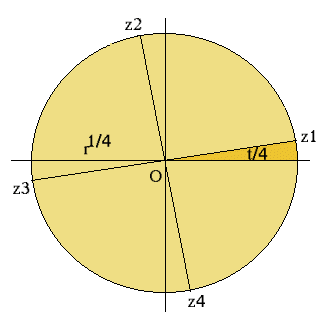
As outras raízes serão:
e todas elas aparecem no gráfico:
Observação: O processo para obter as quatro raízes do número complexo w ficou muito facilitado pois conhecemos a propriedade geométrica que o número complexo i multiplicado por outro número complexo, roda este último de 90 graus e outro fato interessante é que todas as quatro raízes de w estão localizadas sobre a mesma circunferência e os ângulos formados entre duas raízes consecutivas é de 90 graus. Se os quatro números complexos forem ligados, aparecerá um quadrado rodado de t/4 radianos em relação ao eixo OX.
Antes de continuar, apresentaremos a importantíssima
relação de Euler:
que é verdadeira para todo argumento real e a constante e tem o valor aproximado 2,71828... Para facilitar a escrita usamos frequentemente:
Observação: A partir da relação de Euler, é possível construir uma relação notável envolvendo os mais importantes sinais e constantes da Matemática:
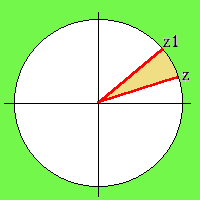
Voltemos agora à exp(i.t). Se multiplicarmos o número ei.t por um número complexo z, o resultado será um outro número complexo rodado de t radianos em relação ao número complexo z. Por exemplo, se multiplicarmos o número complexo z por
obteremos um número complexo z1 que forma com z um ângulo pi/8=22,5o, no sentido
anti-horário.
Iremos agora resolver a equação xn=w, onde n é um número natural e w é um número complexo dado. Da mesma forma que antes, podemos escrever o número complexo
e usar a relação de Euler, para obter:
Para extrair a raiz n-ésima, deve-se construir a primeira raiz que é dada pelo número complexo
Todas as outras n-1 raízes serão obtidas pela multiplicação recursiva dada por:
onde k varia de 2 até n.
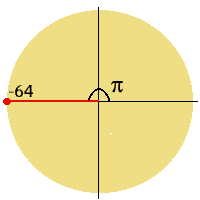
Exemplo: Para obter a primeira raiz da equação x8=-64, observamos a posição do número complexo w = -64 + 0 i, constatando que o seu módulo é igual a 64 e o argumento é um ângulo raso (pi radianos = 180 graus).
Aqui a raiz oitava de 64 é igual a 2 e o argumento da
primeira raiz é pi/8, então z1 pode ser escrita na forma polar:
As outras raízes serão obtidas pela multiplicação do número complexo abaixo,
através de qualquer uma das três formas:
ou ainda pela forma simplificada:
Assim:
Exercício: Construa no sistema cartesiano os 8 números complexos e ligue todas as raízes consecutivas para obter um octógono regular rodado de 22,5 graus em
relação ao eixo OX. Tente comparar este método com outros que você conhece e realize exercícios para observar como aconteceu o aprendizado.
Existe um estudo sobre números complexos, no qual um número complexo z=a+bi pode ser tratado como uma matriz quadrada 2x2 da forma:
e todas as propriedades dos números complexos, podem
ser obtidas através de matrizes, resultando em processos
que transformam as características geométricas dos
números complexos em algo simples.
![]() temos uma série de valores muito simples para as
temos uma série de valores muito simples para as
Potência i2
i3 i4
i5 i6
i7 i8
i9 Valor -1 -i 1 i
-1 -i 1 i
Curiosidade sobre a unidade imaginária
O inverso de um número complexo
b u + a v = 0
v = -b / (a2+b2)
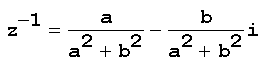
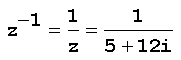
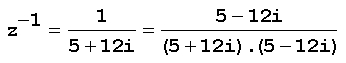
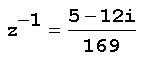
A diferença entre números complexos
A divisão entre números complexos
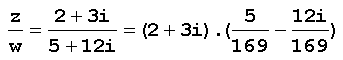
Representação geométrica de um número complexo
Módulo de um número complexo
![]()
![]()
Argumento de um número complexo
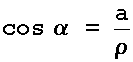
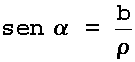
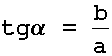
Forma polar de um número complexo
![]()
![]()
Multiplicação de Números complexos na forma polar
w = s (cos n + i sen n)
sen(m+n)={en(m).cos(n)+sen(n).cos(m)
Potência de um Número complexo na forma polar
Raiz quarta de um número complexo
z3 = i . z2
z4 = i . z3
Raiz n-ésima de um número complexo
![]()
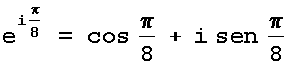
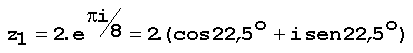
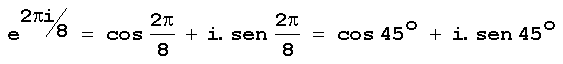
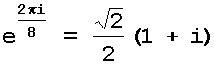
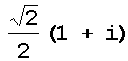
z(3) = z(2).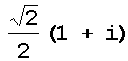
z(4) = z(3).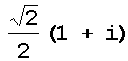
z(5) = z(4).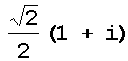
z(6) = z(5).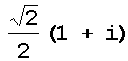
z(7) = z(6).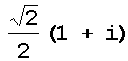
z(8) = z(7).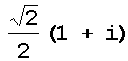
Número complexo como matriz
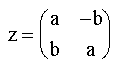
Atualizada em: November 18, 2000.