Consideremos a função real f(x) = 1/x definida para todo x não nulo. O gráfico desta função representa a curva plana chamada hipérbole equilátera, sendo que um ramo da hipérbole está no primeiro quadrante e o outro está localizado no terceiro quadrante. Esta curva tem importantes aplicações em Ótica e construções de óculos, lentes, telescópios, ...

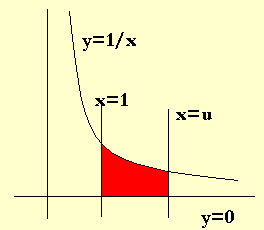
O logaritmo natural de u, denotado por Ln(u), pode ser definido geometricamente, como sendo a área da região plana localizada abaixo do gráfico da curva y=1/x, acima do eixo y=0, entre as retas x=1 e x=u, o que pode ser visto no desenho colorido de vermelho. A área em vermelho representa o logaritmo natural de u, denotado por Ln(u).

Em função do desenho acima, utilizaremos aqui a definição:

Quando u>1, a região possui uma área bem definida, mas se tomarmos u=1, a nossa região se reduzirá a apenas uma linha (que não posssui área ou seja, possui área nula) e neste caso Ln(1)=área(1,1). Assim:

Quando aumentamos os valores de u, esta função também aumenta os seus valores, o que significa que ela é crescente para valores de u>0.

O conceito de Integral de uma função real, normalmente estudado na disciplina Cálculo Diferencial e Integral, justifica a forma como apresentamos o Logaritmo natural de um número real.

Com o uso deste conceito fundamental da Matemática, é possível demonstrar várias propriedades dos Logaritmos naturais (o que não será feito aqui), para números reais positivos x e y e para qualquer número real k, desde que tenham sentido as expressões matemáticas:

• Ln(1) = 0
• Ln(x.y) = Ln(x) + Ln(y)
• Ln(x^k)= k Ln(x)
• Ln(x / y ) = Ln(x) - Ln(y)
• Ln(1/y) = - Ln(y)

As propriedades dos Logaritmos são usadas para simplificar expressões matemáticas, como podemos ver pelos exemplos:

• Ln(5) + 4 Ln(3) = Ln(5) +Ln(3⁴ = Ln(5.3⁴)=Ln(405)
• (1/2)Ln(4t²) -Ln(t) = Ln [(4t²)^1/2]-Ln(t) = Ln(2) Se t>0
• Ln(a) + L(b) - Ln(c) + Ln(10) = Ln( 10a.b/c)

Exercício: Qual dos dois números é o menor: 2 Ln(3) ou 3 Ln(2)? Observa-se que:

e como a função Ln é crescente, então:

Existe um importantíssimo número real e=2,71828... (atribuído a Euler) tal que

A partir da observação anterior, o número e representa a base para os logaritmos naturais e poderemos escrever:

que se lê "logaritmo do número real u na base e".

Tendo em vista a escrita acima, temos uma propriedade que possibilita a mudança logarítmica de uma base positiva para outra base positiva, sendo ambas devem ser diferentes de 1.

Por exemplo, no âmbito do Ensino Médio, usa-se bastante a base 10, uma vez que neste ambiente a base decimal recebe as preferências para o trabalho com o nosso sistema de numeração. Observamos que em contextos mais avançados, a base decimal não é muito útil. Quando escrevermos Log a partir daqui neste trabalho, entenderemos o Logaritmo na base decimal e escrevemos:

para entender que y é o Logaritmo de x na base 10.

de 10

Nesta base 10, temos algumas características interessantes:

A partir da propriedade

temos que o Logaritmo de 10ⁿ na base 10 é o expoente n, o que nos faz pensar que para todo x real positivo vale a relação:

A última expressão mostrada acima é verdadeira e existe uma outra relação muito mais geral do que esta, pois o Logaritmo de um número real positivo x na base b é igual ao número e se, e somente se, x pode ser escrito como a potência b elevada ao expoente e, isto é:

Em livros elementares, esta é tomada como a definição de Logaritmo de um número em uma determinada base, o que é estranho pois tal definição fica como algo cíclico:

• Define-se o logarítmo em função da exponencial;
• Define-se a exponencial em função do logaritmo.

Com esta definição é possível obter o um valor aproximado para o Log(2). Consideremos que y = Log(2) e 10^y=2. Inicialmente, temos que Log(2) é positivo e menor do que 1, pois 1<2<10 assim

É interessante obter dois números que sejam

de 2 e que estejam muito próximos de

de 10.

Por exemplo,

assim, aplicando o logaritmo de base 10, teremos:

e a média aritmética entre 0,300 e 0,308 é 0,304, o que já é uma boa estimativa para Log(2), isto é:

O ideal é encontrar outras

de 10 que estejam próximas de

de 2, o que não é fácil para alguém que não tenha uma calculadora que opere com muitos decimais, o que pode ser visualizado através da tabela mostrando algumas de tais

:

Em estudos de Cálculo Diferencial e Integral, podemos desenvolver a função Log através de uma série de termos e calcular os logaritmos para vários números reais positivos.

Na verdade, Log(2) = 0,3010299956639812... e com este valor, podemos obter os logaritmos de todas as

de 2, como por exemplo:

• Log( 4) = 2 Log(2) = 0,60206
• Log( 8) = 3 Log(2) = 0,90309
• Log(16) = 4 Log(2) = 1,20412
• Log(32) = 5 Log(2) = 1,50515
• Log(64) = 6 Log(2) = 1,80618
• Log(2ⁿ) = n Log(2)
• Log (1/2) =(-1) Log(2) = -0,30103
• Log (1/4) =(-2) Log(2) = -0,60206
• Log (1/8) =(-3) Log(2) = -0,90309
• Log(1/16) =(-4) Log(2) = -1,20412
• Log(1/32) =(-5) Log(2) = -1,50515
• Log(1/64) =(-6) Log(2) = -1,80618
• Log(2^-n) = -n Log(2)

Temos também que Log(3)=0,47712, o que nos permite realizar uma grande quantidade de cálculos com logaritmos.

Com Log(2) e Log3, não é possível calcular os logaritmos dos números primos maiores do que 5, mas é possível obter uma grande quantidade de logaritmos de números naturais.

Exemplo: Vamos usar aqui Log(2)=0,301 e Log(3)=0,477.

• Log(5) = Log(10/2) = Log(10) - Log(2) = 1-0,301 = 0,699
• Log(6) = Log(2.3) = Log(2) + Log(3) = 0,301+0,477=0,778
• Log(8) = Log(2³) = 3 Log(2) = 0,903
• Log(9) = Log(3²) = 2 Log(3) = 0,954

Uma estimativa razoável para Log(7)=0,8451 pode ser obtida com a média entre Log(6) e Log(8), isto é:

Se um número está localizado entre duas

consecutivas de 10, dizemos que o expoente da menor delas é a característica deste logaritmo, enquanto que a diferença entre o logaritmo do número e a característica é a mantissa que é a parte decimal do logaritmo.

log(20) decomposto na característica e mantissa

Notação: Você deve ter observado que na tabela anterior aparece o sinal negativo apenas para o número que está antes da vírgula. Esta notação foi criada para simplificar operações com logaritmos, visando mostrar que se a divisão de dois números é um múltiplo de 10, basta mudar a característica e preservar a mantissa do logaritmo. Isto poderá ser observado na Tábua de logaritmos que aparece no final deste trabalho.

^- 3,30103 significa que o número -3 deve ser somado ao número positivo 0,30103 e isto significa que o resultado deve ser um número com um sinal negativo antes de 2,69897.

• Conjuntos
• Relações e Funções
• Exponenciais
  
• Logaritmos: Teoria
• Logaritmos: Exercícios
  
• Sequências, Progressão Aritmética e Progressão Geométrica
  
• Análise Combinatória: Teoria
• Análise Combinatória: Exercícios
  
• Sistemas Lineares
• Matrizes
• Determinantes
  
• Matrizes 3x3
• Número Complexos
• Equação 3º grau
  
• Formula da Equação de 3º Grau por Tartaglia
• Equação 2o grau
• Produtos Notáveis
• Polinômios